3月6日，记者从市教育局获悉，2018年兰州市高三年级第一次诊断考试将于8日开考，3月8日上午开考语文，下午开考数学，3月9日上午是文综、理综考试，下午是英语考试。

3月3日下午南京市招办召开了高中考体检、中招报名、中考英语听力口语模拟考试考务工作视频会，钱汉平主任再次明确了目前南京市招生考试管理的依据、职责，强调了2015平安招考的工作目标，提出了“凝神聚力、提效守正

六合区中考报名、体检及英语口语模拟考试工作会于3月6日下午在区教育局勤工办三楼会议室顺利召开，参会人员为各初中分管领导、考务员。会议由区招办陈宗朝副主任主持，会议议程如下：1、区招办陈顺立老师传达南京市中

河北石家庄市81中进行模拟考试一年一度的石家庄市区初中毕业生体育考试即将开始，如何让学生们考出更好成绩，日前石家庄81中进行了一场实战模拟考试，从心理上取得了不错效果，学生们对即将到来的考试信心大增。

高三一年有很多的考试，高三学生一定要重视每次考试。以下是高考备考网小编整理有关高三摸底考试的内容，供参考。写给高三：千万千万要重视模拟考试我们现在正在进行紧张有序的模拟考试，经过一个轮次的考试反思回馈

我们在高三的时候，会有很多的考试，有很多同学在一模的时候成绩就不是很好，那么高考模拟考试失利了怎么办呢，请跟随小编来看一下！

相信很多的高三考生是非常的关注高三模拟考试时间表的，小编整理了相关信息，希望会对大家有所帮助！

吉林省高三文综第五次模拟考试试题(含答案)第Ⅰ卷(选择题，共140分)每小题只有一个最符合题意的答案，请选出并把答案涂在答题卡上。(本大题共35小题，每小题4分，总计140分)

2020届江苏高三英语5月第三次模拟考试题

2020届山东省高考化学模拟考试试题

不一样。模拟考试的试题一般都会比正式高考的试题偏难一些，高考很多时候是没有那么难的。作为高三学生一定要正确的去对待模拟考试，不要过度的依赖模拟考试，也不要让模拟考试影响到自己的心态，模拟考试是为了让学

大部分高中，对高三学生的模拟考试是相当重视的，无论是高考之前的一模还是二模，都时刻牵动着高中老师和考生家长的心。那么，高考模拟考试的成绩，与最终的高考成绩相比，到底有多少差距？

方法有时比努力更重要，尤其在高三学习，不要死记硬背，要会分析与总结每次考试的薄弱点在哪？找到薄弱点去攻破它，才能快速提升自己成绩。

有不少高三的同学都在疑惑，为什么到了模拟考试我越考越差了呢？这是什么原因呢？下面是小编整理的详细内容，一起来看看吧！

高考的学生，要经历无数次的平时模拟考试的训练。模拟试卷的难度其实比较高，在没有参加实战高考前夕，模拟试卷就是练兵的法宝。

高考的脚步声越来越近了，大小模拟考试也进行了不少于5次，第一轮的模拟考试，让更多学生意识到基础知识的重要性，第二轮的做题训练，一边巩固基础知识，一边提升做题效率，逐步提升了学生的成绩，但学生最担心的是经

2021高考数学模拟试题

一般来讲,一诊二诊三诊相对高考难度是逐步提升的,第一次模拟考试成绩是与普通高考成绩最为接近的。

学生一般分为三种类型，一种是学习好的，底子扎实，基本不偏科，不管什么难度的题都可以处理的很好；另一种是成绩一般的，有点偏科，而且起伏很大；还有一种是成绩不太好的，基础不牢固，对试卷难易的敏感度也不算太

一诊考试就是学校为了高考做的第一次模拟考试，学校会根据考试成绩来估测高考成绩结果，一诊考试不重要，对高考没影响，只起参照作用。

高三一诊重不能决定高考。一诊考试就是学校为了高考做的第一次模拟考试，学校会根据考试成绩来估测高考成绩结果，一诊考试不重要，对高考没影响，只起参照作用。

一诊的成绩和高考有关系，但是似乎又不太大，一诊考试内容要比正式的高考难一些，覆盖的考点也要多一些，主要目的就是为了刺激学生不要太骄傲，所以，一般来说高考的成绩都会比一诊的成绩高出一些。

成都市2022届高三一诊考试时间是12月27日至12月28日。成都市高三年级的一诊考试一般来说比绵阳市考得晚,大多在每年的12月进行。

一诊考试就是学校为了高考做的第一次模拟考试,学校会根据考试成绩来估测高考成绩结果,一诊考试不重要,对高考没影响。一模是高考前对考生和家长来说都非常重要的一次考试。

高三一诊考试内容要比正式的高考难一些，覆盖的考点也要多一些，主要目的就是为了刺激学生不要太骄傲，所以，一般来说高考的成绩都会比一诊的成绩高出一些。一般来讲，一诊二诊三诊相对高考难度是逐步提升的，第一次

高三一诊考试可以不参加。但一诊有小高考之称,是检测能力的重要考试。大多数人高考成绩与一诊成绩相近,但也有高考成绩比一诊高出很多的情况,这要看一诊之后的努力。

一诊就是一模。整体来说,一模成绩和高考成绩之间存在一定的关系,从一模成绩中能看出孩子在高考中的表现。但是这只是相对而言的,情况比较复杂。

成绩好的学生高三一诊后大约会涨30-50分,因为他们本身成绩就很好,各种考试都可以应付的游刃有余,而一诊的难度本身就比高考要难一些,所以说会涨分,但是幅度不会太大,因为一诊的成绩本身就已经很高了。

首先，应该深度解析自己;其次，仔细分析一诊试卷;最后，清楚自己的优势和劣势。对于比较基础比较薄弱的科目，就不要去钻研它的难题，如数学最后两道大题的最后两个小问、物理最后两道大题的最后两问。对于优势科目则

高三一诊和高考难度接近。不同省份高考前模拟考试的数量不同。一般来说，模拟考试至少有三次。为了检验考生的复习效果，模拟考试的难度将逐步提高。第一次模拟考试的成绩接近高考成绩。

高三一诊考得差怎么激励孩子？要让孩子明白在高三每个阶段都要一直努力，发现自己身上的问题要及时解决。作为父母，千万不要责怪孩子，在不知道怎么做的时候，可以到学校和老师进行沟通，找到恰当的方法，一起帮助孩

要说最接近高考难度的那一定是二诊,一诊考试后发现不足,改正不足,然后在进行一次模拟考试,而一般二诊在高考前半个月进行,目的就是让考生提前适应考试节奏,从体型到涂答题卡都是严格按照高考去进行的,所以说二模的成绩

成都一本文科一诊分数线540.5分、理科493分;南充文科533分、理科502分;德阳文科531分、理科500分;达州文科531分、理科483分。2022四川各地一诊分数线汇总高三一模考试的作用1、一模考试主要就是为了检测一轮复习的效

高三第一次诊断测试的内容比正式高考更难，而且覆盖的考点也更多。主要目的是激励学生不要太骄傲。因此，一般来说，高考分数会高于初诊分数。一般来说，一诊、二诊、三诊的难度相对高考来说是逐渐增加的。第一次模拟

高三一诊成绩差还是能补救的，我们可以利用一诊考是来看看自己哪里不足，制定正确的学习方法，专门攻克自己的弱项，所以一诊没考好也没有什么关系，要关注它反映出的问题，在后边通过努力还是能够补救的。高三一诊成

各位学生和家长不要太在意高三一诊分数，而是要关注它反映出的问题，它是全面复习结束后的一次检测，不仅检测学生学习的效果，更是暴露出学生的问题。让学生去调整自己的学习时间和学习方法，查漏补缺，提升自己，更

高考一模大部分省市地区会安排在3月初，二模考试一般安排在4月初，三模考试一般安排在5月中下旬，有部分地区学校还会组织四模考试。高三模拟考试时间高三一轮复习一般从9月开始。同学们要注意梳理知识点，夯实基础。
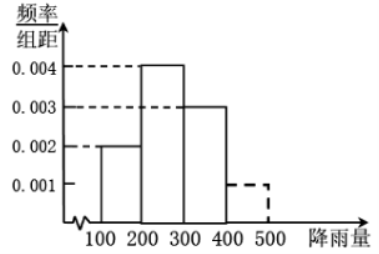
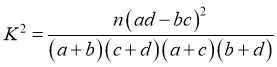
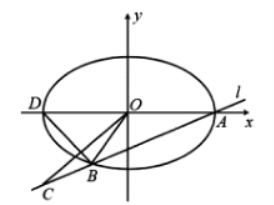
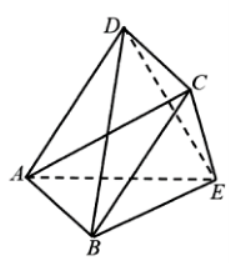
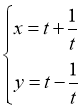
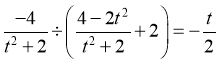
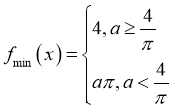