2021年青海高考文科数学真题

2023-01-10 22:07

如有排版混乱问题，请点击下方下载

选择题：本题共12小题，每小题5分，总共60分。在每小题给出的四个选项中，只有一项是符合题目要求的。

已知全集U={1,2,3,4,5},集合M={1,2},N={3,4},则Cu（MUN）=

A.{5}

B.{1,2}

C.{3,4}

D.{1,2,3,4}

2.设iz=4+3i，则z等于

A.-3-4i

B.-3+4i

C.3-4i

D.3+4i

3.已知命题

，sinx<1，命题

e|x|

1，则下列命题中为真命题的是

A.p

q

B.

p

q

C.p

q

D.

(p

q)

4.函数f（x）=sin

+cos

的最小正周期和最大值分别是

A.3

和

B.3

和2

C.

和

D.

和2

5.若x，y满足约束条件

,则z=3x+y的最小值为

A.18

B.10

C.6

D.4

6.

A.

B.

C.

D.

7.在区间(0,

)随机取1个数，则取到的数小于

的概率为

A.

B.

C.

D.

8.下列函数中最小值为4的是

A.

B.

C.

D.

9.设函数

，则下列函数中为奇函数的是

A.

B.

C.

D.

10.在正方体ABCD-A1B1C1D1，P为B1D1的重点，则直线PB与AD1所成的角为

A.

B.

C.

D.

11.设B是椭圆C：

的上顶点，点P在C上，则|PB|的最大值为

A.

B.

C.

D.2

12.设

,若

为函数f(x)=

的极大值点，则

A.a<b

B.a>b

C.ab<

D. ab>

二、填空题：本题共4小题，每小题5分，共20分

13.已知向量a=(2,5),b=(λ,4)，若

，则λ=________.

14.双曲线

的右焦点到直线x+2y-8=0的距离为_________.

15.记

的内角A，B，C的对边分别为a，b，c，面积为

，B=

，

，则b=_______.

16.以图①为正视图，在图②③④⑤中选两个分别作为侧视图和俯视图，组成某个三棱锥的三视图，则所选侧视图和俯视图的编号依次为（写出符合要求的一组答案即可）。

2021年青海高考文科数学真题

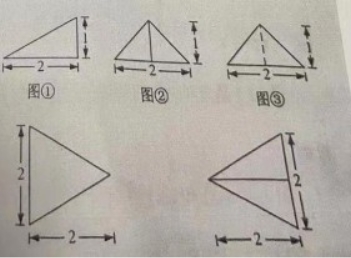
三、解答题

（一）必考题

17.（12分）

某厂研制了一种生产高精产品的设备，为检验新设备生产产品的某项指标有无提高，用一台旧设备和一台新设备各生产了10件产品，得到各件产品该项指标数据如下：

2021年青海高考文科数学真题

旧设备和新设备生产产品的该项指标的样本平均数分别为

和

,样本方差分别记为

和

.

（1）求

，

，

，

（2）判断新设备生产产品的该项指标的均值较旧设备是否有显著提高（如果）

，则认为新设备生产产品的该项指标的均值较旧设备有显著提高，否则不认为有显著提高）.

18. （12分）

如图，四棱锥P-ABCD的底面是矩形，PD

底面ABCD，M为BC的中点，且PB

AM.

证明：平面PAM

平面PBD；

若PD=DC=1，求四棱锥P-ADCD的体积.

2021年青海高考文科数学真题

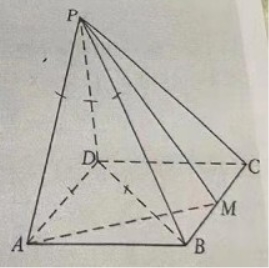
19.(12分)

设

是首项为1的等比数列，数列

满足

，已知

，3

，9

成等差数列.

(1)求

和

的通项公式；

(2)记

和

分别为

和

的前n项和.证明：

<

.

20.（12分）

已知抛物线C：

(p>0)的焦点F到准线的距离为2.

求C的方程.

已知O为坐标原点，点P在C上，点Q满足

，求直线OQ斜率的最大值.

21.（12分）

已知函数

.

（1）讨论

的单调性；

（2）求曲线

过坐标原点的切线与曲线

的公共点的坐标.

（二）选考题：共10分。请考生在第22、23题中任选一题作答。如果多做，则按所做的第一题计分。

22.[选修4-4：坐标系与参数方程]（10分）

在直角坐标系

中，

的圆心为

，半径为1.

（1）写出

的一个参数方程。

（2）过点

作

的两条切线，以坐标原点为极点，

轴正半轴为极轴建立极坐标系，求这两条切线的极坐标方程。

23.[选修4-5：不等式选讲]（10分）

已知函数

.

（1）当

时，求不等式

的解集；

（2）若

，求

的取值范围.

相关专题：青海高考